Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали любого прямоугольника делят его на 4 равных треугольника.
3) Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.
Рассмотрим каждое утверждение:
1) "
Медиана
равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию", это утверждение верно, т.к. это
свойство
равнобедренного треугольника.
2) "Диагонали любого прямоугольника делят его на 4 равных треугольника", это утверждение неверно, т.к. у равных треугольников равны все стороны, а одна из сторон треугольников совпадает с одной из стороной прямоугольника. А соседние стороны прямоугольника могут быть не равны друг другу, тогда и стороны треугольников будут не равны, а значит и неравны сами треугольники.
3) "Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса", это утверждение верно, это становится очевидным, если провести радиус через эту точку.
Поделитесь решением
Присоединяйтесь к нам...
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
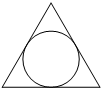Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
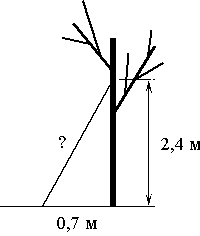Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: