На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
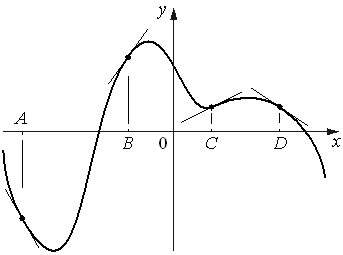
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| А | 1) -0,7 |
| B | 2) 1,4 |
| C | 3) -1,8 |
| D | 4) 0,5 |
Производную от функции, в данном случае, лучше рассматривать как тангенс угла наклона касательной.
Если тангенс положительный (т.е. угол острый), то и производная положительна и наоборот.
Тогда сразу можно сказать, что в точках B и C - значение производной положительно.
А в точках A и D - отрицательно.
Если посмотреть на таблицу углов, то ставится понятно, что при увеличени угла значение тангенса увеличивается (tg0°=0, tg45°=1, tg90°=+∞).
Следовательно, значение тангенса в точке B больше значения тангенса в точке C.
Получаем, что:
В точке B - значение производной равно 1,4.
В точке C - значение производной равно 0,5.
При дальнейшем увеличении угла (от 90° до 180°) значение тангенса меняется от -∞ до 0, т.е. уменьшается по модулю.
Следовательно, в точке A значение производной равно -1,8, а в точке D - значение производной равно -0,7.
Ответ:
| A | B | C | D |
| 3) | 2) | 4) | 1) |
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| А | 1) -0,7 |
| B | 2) 1,4 |
| C | 3) -1,8 |
| D | 4) 0,5 |
На рисунке точками показано атмосферное давление в городе N
на протяжении трёх суток с 4 по 6 апреля 2013 года. В течение суток давление измеряется 4 раза: в 00:00, в 06:00, в 12:00 и в 18:00.
По горизонтали указывается время суток и дата, по вертикали — давление
в миллиметрах ртутного столба. Для наглядности точки соединены линией.
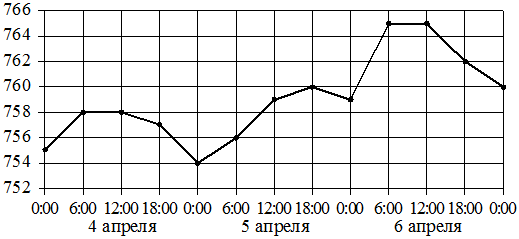
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику атмосферного давления в городе N
в течение этого периода.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) утро 4 апреля (с 6 до 12 часов) | 1) давление не менялось и было выше 764 мм рт. ст. |
| Б) утро 5 апреля (с 6 до 12 часов) | 2) давление росло |
| В) утро 6 апреля (с 6 до 12 часов) | 3) давление не менялось и было ниже 760 мм рт. ст. |
| Г) день 6 апреля (с 12 до 18 часов) | 4) давление падало |
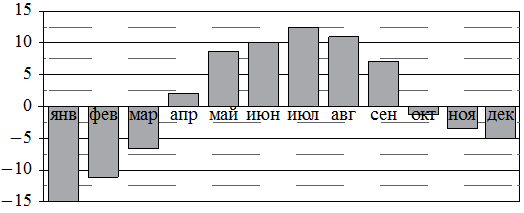На диаграмме показана среднемесячная температура воздуха
в Петрозаводске за каждый месяц 1976 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия.
Определите по диаграмме наименьшую среднемесячную температуру
во второй половине 1976 года. Ответ дайте в градусах Цельсия.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| А | 1) -0,7 |
| B | 2) 1,4 |
| C | 3) -1,8 |
| D | 4) 0,5 |
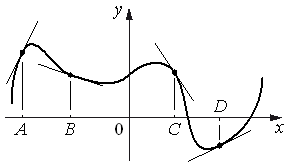На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A | 1) -1,5 |
| B | 2) 0,5 |
| C | 3) 2 |
| D | 4) -0,3 |
Хочу получать новые решения
Ни какого спама
| α | sinα | cosα | tgα | ctgα |
| 0° | 0 | 1 | 0 | --- |
| 30° | 1/2 | √ |
√ |
√ |
| 45° | √ |
√ |
1 | 1 |
| 60° | √ |
1/2 | √ |
√ |
| 90° | 1 | 0 | --- | 0 |
| 120° | √ |
-1/2 | -√ |
0 |
| 135° | √ |
-√ |
-1 | -1 |
| 150° | 1/2 | -√ |
-√ |
-√ |
| 180° | 0 | -1 | 0 | --- |
| 210° | -1/2 | -√ |
√ |
√ |
| 225° | -√ |
-√ |
1 | 1 |
| 240° | -√ |
-1/2 | √ |
√ |
| 270° | -1 | 0 | --- | 0 |
| 300° | -√ |
1/2 | -√ |
-√ |
| 315° | -√ |
√ |
-1 | -1 |
| 330° | -1/2 | √ |
-√ |
-√ |
| 360° | 1 | 0 | 0 | --- |
Автор: Таська
Комментарии: