
 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
По
определению тангенса, tgB=7/2=3,5
Ответ: tgB=3,5.
Поделитесь решением
Присоединяйтесь к нам...
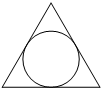 Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
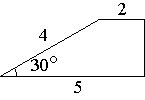 Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
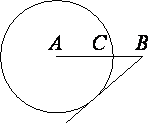 На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.





Комментарии:
(2015-05-21 20:40:29) Администратор: Лена, по определению tg - это отношение ПРОТИВОлежащего катета к ПРИлежащему, поэтому 7/2.
(2015-05-20 16:30:44) Лена: Почему 7/2,а не 2/7?