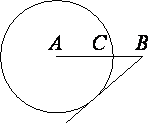На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
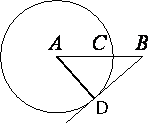Проведем отрезок AD, где D - точка касания
окружности и
касательной.
AD перпендикулярен к
касательной (по
свойству касательной), т.е. угол между AD и
касательной DB равен 90°.
Следовательно, треугольник ABD -
прямоугольный.
AD=AC=14 (т.к. это радиусы окружности и, соответственно, равны друг другу).
По
теореме Пифагора: AB2=AD2+BD2
(AC+BC)2=AD2+BD2
(14+36)2=142+BD2
2500=196+BD2
BD2=2304
BD=48
Ответ: длина касательной равна 48.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC.
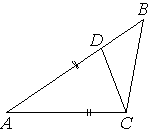Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
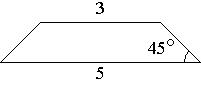В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: