
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ407 –Η–Ζ 1087 |
 –ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ ―²―Ä–Α–Ω–Β―Ü–Η–Η
ABCD, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Β―ë –±–Ψ–Κ–Ψ–≤―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CD –≤ ―²–Ψ―΅–Κ–Α―Ö E –Η F ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –Ψ―²―Ä–Β–Ζ–Κ–Α EF, –Β―¹–Μ–Η AD=42, BC=14, CF:DF=4:3.
–ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ ―²―Ä–Α–Ω–Β―Ü–Η–Η
ABCD, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Β―ë –±–Ψ–Κ–Ψ–≤―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CD –≤ ―²–Ψ―΅–Κ–Α―Ö E –Η F ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –Ψ―²―Ä–Β–Ζ–Κ–Α EF, –Β―¹–Μ–Η AD=42, BC=14, CF:DF=4:3.
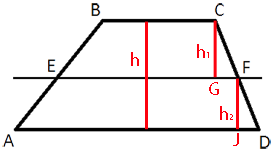 –ü―Ä–Ψ–≤–Β–¥–Β–Φ
–≤―΄―¹–Ψ―²―΄ h1 –Η h2 –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ
–≤―΄―¹–Ψ―²―΄ h1 –Η h2 –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η CFG –Η FDJ.
∠CGF=∠FJD=90¬Α (―².–Κ. –Φ―΄ –Ω―Ä–Ψ–≤–Ψ–¥–Η–Μ–Η
–≤―΄―¹–Ψ―²―΄).
∠CFG=∠FDJ (―².–Κ. ―ç―²–Ψ
―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ―΄–Β ―É–≥–Μ―΄).
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, ―ç―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η
–Ω–Ψ–¥–Ψ–±–Ϋ―΄ –Ω–Ψ
–Ω–Β―Ä–≤–Ψ–Φ―É –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É –Ω–Ψ–¥–Ψ–±–Η―è.
–ü–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é –Ω–Ψ–¥–Ψ–±–Ϋ―΄―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤:
CF/DF=CG/FJ=4/3
–î–Μ―è –Ω―Ä–Ψ―¹―²–Ψ―²―΄ –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ:
CG=h1
FJ=h2
SEBCF=(CB+EF)*h1/2
SAEFD=(EF+AD)*h2/2
SABCD=(BC+AD)*(h1+h2)/2
–Δ–Α–Κ ―¹―É–Φ–Φ–Α –Ω–Μ–Ψ―â–Α–¥–Β–Ι ―ç―²–Η―Ö
―²―Ä–Α–Ω–Β―Ü–Η–Ι ―Ä–Α–≤–Ϋ–Α –Ω–Μ–Ψ―â–Α–¥–Η –±–Ψ–Μ―¨―à–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η, ―²–Ψ –Ζ–Α–Ω–Η―à–Β–Φ:
(CB+EF)*h1/2+(EF+AD)*h2/2=(BC+AD)*(h1+h2)/2
(CB+EF)*h1+(EF+AD)*h2=(BC+AD)*(h1+h2)
CB*h1+EF*h1+EF*h2+AD*h2=BC*h1+BC*h2+AD*h1+AD*h2
CB*h1+EF*h1-BC*h1-AD*h1=BC*h2+AD*h2-EF*h2-AD*h2
(CB+EF-BC-AD)*h1=(BC+AD-EF-AD)*h2
(EF-AD)*h1=(BC-EF)*h2
h1/h2=(BC-EF)/(EF-AD)
4/3=(14-EF)/(EF-42)
4(EF-42)=3(14-EF)
4*EF-168=42-3*EF
7*EF=210
EF=30
–û―²–≤–Β―²: EF=30
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD AB=CD, AC=AD –Η ∠ABC=95¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ CAD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD AB=CD, AC=AD –Η ∠ABC=95¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ CAD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –ù–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Β AB ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –≤–Ζ―è―²–Α ―²–Ψ―΅–Κ–Α D ―²–Α–Κ, ―΅―²–Ψ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Α―è ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ–Η A, C –Η D, –Κ–Α―¹–Α–Β―²―¹―è –Ω―Ä―è–Φ–Ψ–Ι BC. –ù–Α–Ι–¥–Η―²–Β AD, –Β―¹–Μ–Η AC=12, BC=18 –Η CD=8.
–ù–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Β AB ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –≤–Ζ―è―²–Α ―²–Ψ―΅–Κ–Α D ―²–Α–Κ, ―΅―²–Ψ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Α―è ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ–Η A, C –Η D, –Κ–Α―¹–Α–Β―²―¹―è –Ω―Ä―è–Φ–Ψ–Ι BC. –ù–Α–Ι–¥–Η―²–Β AD, –Β―¹–Μ–Η AC=12, BC=18 –Η CD=8.
 –ù–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Ω–Ψ ―Ä–Α–Ζ–Ϋ―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –Ψ―² –¥–Η–Α–Φ–Β―²―Ä–Α AB –≤–Ζ―è―²―΄ ―²–Ψ―΅–Κ–Η M –Η N. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ
∠NBA=64¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ NMB. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ù–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Ω–Ψ ―Ä–Α–Ζ–Ϋ―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –Ψ―² –¥–Η–Α–Φ–Β―²―Ä–Α AB –≤–Ζ―è―²―΄ ―²–Ψ―΅–Κ–Η M –Η N. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ
∠NBA=64¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ NMB. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –ù–Α –Κ–Α–Κ–Ψ–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η (–≤ –Φ–Β―²―Ä–Α―Ö) –Ψ―² ―³–Ψ–Ϋ–Α―Ä―è ―¹―²–Ψ–Η―² ―΅–Β–Μ–Ψ–≤–Β–Κ ―Ä–Ψ―¹―²–Ψ–Φ 1,8 –Φ, –Β―¹–Μ–Η –¥–Μ–Η–Ϋ–Α –Β–≥–Ψ ―²–Β–Ϋ–Η ―Ä–Α–≤–Ϋ–Α 9 –Φ, –≤―΄―¹–Ψ―²–Α ―³–Ψ–Ϋ–Α―Ä―è 5 –Φ?
–ù–Α –Κ–Α–Κ–Ψ–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η (–≤ –Φ–Β―²―Ä–Α―Ö) –Ψ―² ―³–Ψ–Ϋ–Α―Ä―è ―¹―²–Ψ–Η―² ―΅–Β–Μ–Ψ–≤–Β–Κ ―Ä–Ψ―¹―²–Ψ–Φ 1,8 –Φ, –Β―¹–Μ–Η –¥–Μ–Η–Ϋ–Α –Β–≥–Ψ ―²–Β–Ϋ–Η ―Ä–Α–≤–Ϋ–Α 9 –Φ, –≤―΄―¹–Ψ―²–Α ―³–Ψ–Ϋ–Α―Ä―è 5 –Φ?
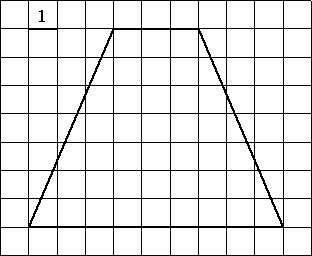 –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–Ι –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–Ι –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.



–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2017-03-06 23:30:43) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –ê–Μ–Η–Ϋ–Α, –€―΄ –Ϋ–Β –Ω–Ψ–Φ–Ψ–≥–Α–Β–Φ ―Ä–Β―à–Η―²―¨ –¥–Ψ–Φ–Α―à–Ϋ–Β–Β –Ζ–Α–¥–Α–Ϋ–Η–Β, ―Ü–Β–Μ―¨ ―¹–Α–Ι―²–Α - –Ω–Ψ–¥―Ä–Ψ–±–Ϋ–Ψ ―Ä–Α–Ζ–Ψ–±―Ä–Α―²―¨ –Ζ–Α–¥–Α―΅–Η, –Κ–Ψ―²–Ψ―Ä―΄–Β –±―É–¥―É―² –Ϋ–Α ―ç–Κ–Ζ–Α–Φ–Β–Ϋ–Α―Ö, ―΅―²–Ψ–±―΄ ―É―΅–Α―â–Η–Β―¹―è –Ϋ–Α―É―΅–Η–Μ–Η―¹―¨ –Η―Ö ―Ä–Β―à–Α―²―¨ ―¹–Α–Φ–Ψ―¹―²–Ψ―è―²–Β–Μ―¨–Ϋ–Ψ. –ï―¹–Μ–Η –Ϋ–Α–Ι–¥–Β―²–Β –Ω–Ψ―Ö–Ψ–Ε―É―é –Ζ–Α–¥–Α―΅―É –Ϋ–Α ―¹–Α–Ι―²–Β fipi.ru, –Ψ―²–Ω―Ä–Α–≤―²–Β –Ζ–Α―è–≤–Κ―É –Ϋ–Α –¥–Ψ–±–Α–≤–Μ–Β–Ϋ–Η–Β –Ζ–Α–¥–Α―΅–Η, –Η –Φ―΄ –Β–Β –Ψ–±―è–Ζ–Α―²–Β–Μ―¨–Ϋ–Ψ –¥–Ψ–±–Α–≤–Η–Φ.
(2017-03-06 11:04:23) –ê–¦–‰–ù–ê: –Ϋ–Α –Ω―Ä―è–Φ–Ψ–Ι –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ –Ψ―²–Φ–Β―΅–Β–Ϋ―΄ ―²–Ψ―΅–Κ–Η L,K,P,F,E,―²–Α–Κ ―΅―²–Ψ LK=KP=PF=FE=2―¹–Φ.–ö–Α–Κ–Η–Β –Β―â―ë ―Ä–Α–≤–Ϋ―΄–Β –Ψ―²―Ä–Β–Ζ–Κ–Η –Ψ–Ω―Ä–Β–¥–Β–Μ―è―é―²―¹―è –Ω–Ψ ―ç―²–Η–Φ ―²–Ψ―΅–Κ–Α–Φ?–½–Α–Ω–Η―¹–Α―²―¨ ―ç―²–Η –Ψ―²―Ä–Β–Ζ–Κ–Η –Η –Ϋ–Α–Ι―²–Η –Η―Ö –¥–Μ–Η–Ϋ―΄
(2016-12-18 20:10:06) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –£–Β―Ä–Ψ–Ϋ–Η–Κ–Α, –Α–Ϋ–Α–Μ–Ψ–≥–Η―΅–Ϋ–Ψ ―ç―²–Ψ–Ι.
(2016-12-18 18:45:22) –£–Β―Ä–Ψ–Ϋ–Η–Κ–Α: ⳕ 4) –ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ ―²―Ä–Α–Ω–Β―Ü–Η–Η –ê–£–ΓD, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Β―ë –±–Ψ–Κ–Ψ–≤―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –ê–£ –Η –ΓD –≤ ―²–Ψ―΅–Κ–Α―Ö –ï –Η F ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –Ψ―²―Ä–Β–Ζ–Κ–Α –ïF, –Β―¹–Μ–Η –êD = 45, –£–Γ = 20, –ΓF : DF = 4 : 1. –ö–Α–Κ ―Ä–Β―à–Η―²―¨ ―ç―²―É –Ζ–Α–¥–Α―΅―É ?
(2015-05-10 19:03:07) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –€–Α―Ä–Η―è, ―è –¥–Ψ–Ω–Η―¹–Α–Μ –≤ ―Ä–Β―à–Β–Ϋ–Η–Β –Ω–Α―Ä―É ―¹―²―Ä–Ψ–Κ, ―΅―²–Ψ–±―΄ ―¹―²–Α–Μ–Ψ –Ω–Ψ–Ϋ―è―²–Ϋ–Β–Ι.
(2015-05-10 16:28:56) –€–Α―Ä–Η―è: –ü–Ψ–Φ–Ψ–≥–Η―²–Β –Ω–Ψ–Ε–Α–Μ―É–Ι―¹―²–Α, –Κ–Α–Κ –Η–Ζ (CB+EF)*h1+(EF+AD)*h2=(BC+AD)*(h1+h2) –Ω–Ψ–Μ―É―΅–Η–Μ–Ψ―¹―¨ (CB+EF-BC-AD)*h1=(BC+AD-EF-AD)*h2 ?
(2015-05-09 14:45:52) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –ï–Μ–Β–Ϋ–Α, –Ψ―²–Μ–Η―΅–Ϋ―΄–Ι –≤–Α―Ä–Η–Α–Ϋ―², ―¹–Κ–Ψ―Ä–Ψ –Β–≥–Ψ –Ψ–Ω―É–±–Μ–Η–Κ―É―é, ―¹–Ω–Α―¹–Η–±–Ψ!
(2015-05-08 21:51:36) –ï–Μ–Β–Ϋ–Α: –ü―Ä–Ψ–≤–Β–¥―ë–Φ –Η–Ζ –≤–Β―Ä―à–Η–Ϋ―΄ –Γ –Ω―Ä―è–Φ―É―é –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―É―é –ê–£. –û–Ϋ–Α ―Ä–Α–Ζ–Ψ–±―¨―ë―² –êD –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η, ―Ä–Α–≤–Ϋ―΄–Β 14 –Η 28 , –Α EF –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η 14 –Η ―Ö. –Δ―Ä–Α–Ω–Β―Ü–Η―è –±―É–¥–Β―² ―Ä–Α–Ζ–¥–Β–Μ–Β–Ϋ–Α –Ϋ–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ –Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ. –ü―Ä―è–Φ–Α―è EF –¥–Β–Μ–Η―² ―ç―²–Ψ―² ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –Ϋ–Α –¥–≤–Α –Ω–Ψ–¥–Ψ–±–Ϋ―΄―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α. –ö–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―² –Ω–Ψ–¥–Ψ–±–Η―è 4/7. ―Ö=16, ―²–Ψ–≥–¥–Α EF=14+16=30