Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
Площадь
ромба равна S=ah, где a - сторона ромба, h - высота ромба.
AD=AH+HD=21+8=29.
AD=AB=BC=CD (по
определению ромба).
Рассмотрим треугольник ABH.
ABH -
прямоугольный (т.к. BH -
высота), тогда по
теореме Пифагора: AB2=BH2+AH2
292=BH2+212
841=BH2+441
BH2=400
BH=20
Sромба=AD*BH=29*20=580
Ответ: Sромба=580
Поделитесь решением
Присоединяйтесь к нам...
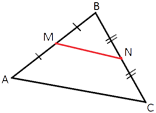Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
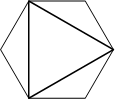Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
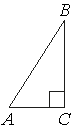В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Площадь прямоугольного треугольника равна 882√
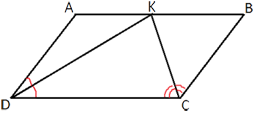Биссектрисы углов C и D параллелограмма ABCD пересекаются в точке K стороны AB. Докажите, что K — середина AB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: