На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.
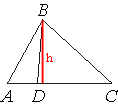Проведем высоту из вершины B.
Заметим, что это высота не только треугольника ABC, но и треугольника ABD.
Найдем высоту, используя формулу площади треугольника для треугольника ABC:
SABC=AC*h/2=(AD+DC)*h/2
60=(5+7)*h/2
60=12*h/2
60=6*h
h=10
Теперь применим эту же формулу для треугольника ABD:
SABD=AD*h/2=5*10/2=5*5=25
Ответ: 25
Поделитесь решением
Присоединяйтесь к нам...
Площадь параллелограмма ABCD равна 5. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
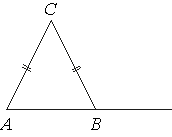В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
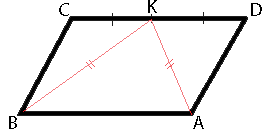В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: