
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 1 м, высота фонаря 9 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 1 м, высота фонаря 9 м?
 Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE, эти треугольники
подобны, т.к. /C - общий, /B и /DEC - прямые, а углы A и EDC - равны, так как являются
соответственними.
Из подобия этих треугольников следует, что AB/DE=BC/EC,
AB/DE=(BE+EC)/EC, отсюда (AB*EC)/DE=BE+EC
BE=(AB*EC)/DE-EC
BE=(9*1)/1,8-1=4
Ответ: расстояние от фонаря до человека 4 м.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
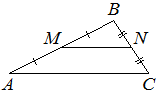 Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.
 В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
 Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
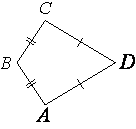 В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
Комментарии: