
 Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
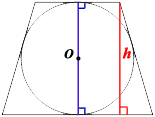 Проведем высоту
трапеции (красный отрезок). Высота перпендикулярна обоим основаниям (по определению).
Проведем высоту
трапеции (красный отрезок). Высота перпендикулярна обоим основаниям (по определению).
Проведем радиусы окружности к обоим основаниям (синие отрезки).
Очевидно, что радиусы, высота и основания образуют прямоугольник, следовательно, радиусы образуют диаметр, который равен высоте.
h=D=2R=2*20=40.
Ответ: 40
Поделитесь решением
Присоединяйтесь к нам...
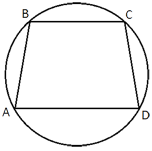 Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
 В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 67. Найдите площадь четырёхугольника ABMN.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 67. Найдите площадь четырёхугольника ABMN.
 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
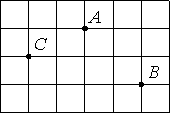 На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
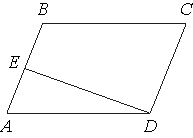 Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Комментарии:
(2021-05-25 11:19:48) рината: найдите площадь изображенной на клетчатой бумаге с размером клетки 2х2 см.