Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
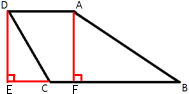Дочертим отрезки как показано на рисунке.
DE=AF, т.к. это
высоты
трапеции.
∠DCE=180°-∠BCD=180°-150°=30° (т.к. это
смежные углы).
sin(∠DCE)=ED/CD (по
определению)
sin30°=ED/CD (sin30°=1/2 по
таблице)
1/2=ED/33
ED=33*1/2=16,5
sin(∠ABF)=AF/AB (по
определению)
sin60°=ED/AB
AB=ED/sin60° (sin60°=√3/2 по
таблице)
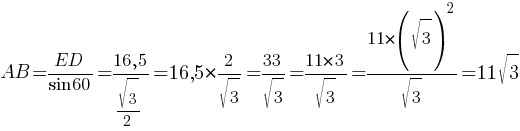
Ответ: 11√3
Поделитесь решением
Присоединяйтесь к нам...
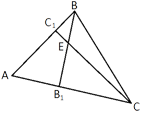Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
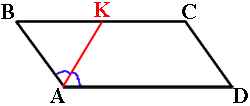Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
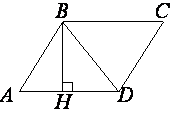Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: