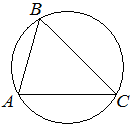
В треугольнике ABC угол C равен 45°, AB=6√
По
теореме синусов:
AB/sin∠C=2R
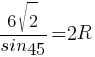
sin45=√
√
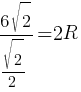
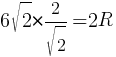
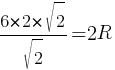
12=2R
R=6
Ответ: 6
Поделитесь решением
Присоединяйтесь к нам...
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
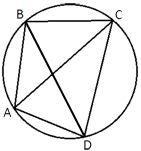Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
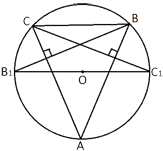Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-12-19 10:42:50) Тимур: В треугольнике ABC угол А =135 градусов, АВ =2 Корней из 2, АС=3 найдите ВС
(2021-04-07 16:24:10) кристина: в треугольнике ABC угол C=90 угол A=30 AB= 26 найдите длину стороны AB