
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ86 –ł–∑ 1087 |
–°—ā–ĺ—Ä–ĺ–Ĺ—č AC, AB, BC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC —Ä–į–≤–Ĺ—č 3√
 –ü–ĺ —É—Ā–Ľ–ĺ–≤–ł—é –∑–į–ī–į—á–ł /KAC>90¬į, —ā.–Ķ. —ć—ā–ĺ –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ AKC —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —Ā—ā–ĺ—Ä–ĺ–Ĺ–į KC, –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ľ–Ķ–∂–į—Č–į—Ź —ć—ā–ĺ–ľ—É —É–≥–Ľ—É —ā–ĺ–∂–Ķ –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–į—Ź (–Ņ–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ĺ —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź—Ö –ľ–Ķ–∂–ī—É —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ–ł –ł —É–≥–Ľ–į–ľ–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į). –°—ā–ĺ—Ä–ĺ–Ĺ–į AC —Ä–į–≤–Ĺ–į—Ź 3√
–ü–ĺ —É—Ā–Ľ–ĺ–≤–ł—é –∑–į–ī–į—á–ł /KAC>90¬į, —ā.–Ķ. —ć—ā–ĺ –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ AKC —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —Ā—ā–ĺ—Ä–ĺ–Ĺ–į KC, –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ľ–Ķ–∂–į—Č–į—Ź —ć—ā–ĺ–ľ—É —É–≥–Ľ—É —ā–ĺ–∂–Ķ –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–į—Ź (–Ņ–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ĺ —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź—Ö –ľ–Ķ–∂–ī—É —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ–ł –ł —É–≥–Ľ–į–ľ–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į). –°—ā–ĺ—Ä–ĺ–Ĺ–į AC —Ä–į–≤–Ĺ–į—Ź 3√
–ü–ĺ —É—Ā–Ľ–ĺ–≤–ł—é –∑–į–ī–į—á–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ KAC –Ņ–ĺ–ī–ĺ–Ī–Ķ–Ĺ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–ľ—É —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ—É ABC. –ź –∑–Ĺ–į—á–ł—ā —É–≥–Ľ—č —ć—ā–ł—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ —Ä–į–≤–Ĺ—č (–Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤). –ü–ĺ—ć—ā–ĺ–ľ—É –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–ł–Ķ —É–≥–Ľ—č –ī–≤—É—Ö —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ—č—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤ —Ä–į–≤–Ĺ—č, —ā.–Ķ. /KAC=/ABC. /ACK –Ĺ–Ķ —Ä–į–≤–Ķ–Ĺ /ACB ( —ā.–ļ. KC –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É AB –≤ —ā–ĺ—á–ļ–Ķ, –ĺ—ā–Ľ–ł—á–Ĺ–ĺ–Ļ –ĺ—ā B), –Ņ–ĺ—ć—ā–ĺ–ľ—É /ACK = /BAC. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, /AKC=/ACB => cos(/AKC)=cos(/ACB).
–ü—Ä–ł–ľ–Ķ–Ĺ—Ź—Ź —ā–Ķ–ĺ—Ä–Ķ–ľ—É –ļ–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤ –ľ—č –ľ–ĺ–∂–Ķ–ľ –∑–į–Ņ–ł—Ā–į—ā—Ć AB2=AC2+BC2-2*AC*BC*cos(/ACB).
(√
15=9*2+1-6*√
15-19=-6*√
4=6*√
cos(/AKC)=cos(/ACB)=4/(6*√
cos(/AKC)=cos(/ACB)=2/(3*√
cos(/AKC)=√
–ě—ā–≤–Ķ—ā: cos(/AKC)=√
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –ö–į—ā–Ķ—ā—č –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ—č 2√
–ö–į—ā–Ķ—ā—č –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ—č 2√
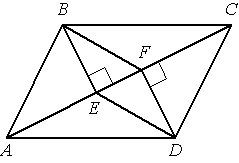 –í –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–Ķ –ź–í–°D –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä—č –í–ē –ł DF –ļ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł –ź–° (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł BEF –ł DFE —Ä–į–≤–Ĺ—č.
–í –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–Ķ –ź–í–°D –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä—č –í–ē –ł DF –ļ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł –ź–° (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł BEF –ł DFE —Ä–į–≤–Ĺ—č.
 –†–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ O —Ä–į–≤–Ķ–Ĺ 50, –ī–Ľ–ł–Ĺ–į —Ö–ĺ—Ä–ī—č AB —Ä–į–≤–Ĺ–į 96 (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —Ö–ĺ—Ä–ī—č AB –ī–ĺ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –Ķ–Ļ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ k.
–†–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ O —Ä–į–≤–Ķ–Ĺ 50, –ī–Ľ–ł–Ĺ–į —Ö–ĺ—Ä–ī—č AB —Ä–į–≤–Ĺ–į 96 (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —Ö–ĺ—Ä–ī—č AB –ī–ĺ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –Ķ–Ļ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ k.
 –í –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–Ķ ABCD –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć AC –≤ 2 —Ä–į–∑–į –Ī–ĺ–Ľ—Ć—ą–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł ∠ACD=1¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ź–ľ–ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–í –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–Ķ ABCD –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć AC –≤ 2 —Ä–į–∑–į –Ī–ĺ–Ľ—Ć—ą–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł ∠ACD=1¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ź–ľ–ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
 –†–į–ī–ł—É—Ā –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ –ļ–≤–į–ī—Ä–į—ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 14√
–†–į–ī–ł—É—Ā –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ –ļ–≤–į–ī—Ä–į—ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 14√
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: