
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Рассмотрим треугольник BDH.
Данный треугольник
прямоугольный, следовательно можно применить
теорему Пифагора:
BD2=HD2+BH2
532=282+BH2
2809=784+BH2
BH2=2025
BH=45
Найдем площадь
параллелограмма:
S=AD*BH=(AH+HD)*BH=(1+28)*45=1305
Ответ: 1305
Поделитесь решением
Присоединяйтесь к нам...
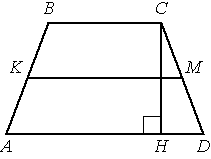 В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
 Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
 Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
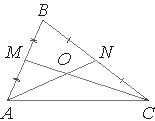 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Комментарии: