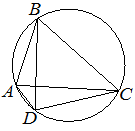
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
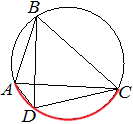∠ABC является вписанным углом и опирается на дугу ADC (красная).
Следовательно, по теореме о вписанном угле, градусная мера дуги ADC равна 70°*2=140°
∠CAD тоже является вписанным углом и опирается на дугу DC.
Следовательно, по теореме о вписанном угле, градусная мера дуги DC равна 49°*2=98°
Тогда легко вычислить градусную меру дуги AD:
140°-98°=42°
Искомый ∠ABD тоже является вписанным углом и опирается на дугу AD.
Следовательно, по теореме о вписанном угле, угол ABD равен:
42°/2=21°
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
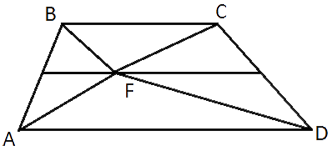На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
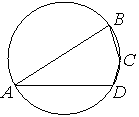Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: