Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
Так как сторона AC треугольника ABC проходит через центр
описанной около него окружности, то AC - это диаметр окружности.
Следовательно, треугольник ABC - прямоугольный (по
свойству описанной окружности), т.е. ∠B=90°.
По
теореме о сумме углов треугольника:
∠A+∠B+∠C=180°
81°+90°+∠C=180°
∠C=180°-81°-90°
∠C=9°
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
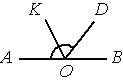Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=52°. Ответ дайте в градусах.
Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
В трапеции ABCD AD=3, BC=1, а её площадь равна 12. Найдите площадь треугольника ABC.
Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
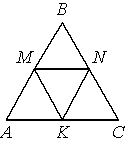В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: