
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ78 –Η–Ζ 1087 |
 –ù–Α –Κ–Α–Κ–Ψ–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η (–≤ –Φ–Β―²―Ä–Α―Ö) –Ψ―² ―³–Ψ–Ϋ–Α―Ä―è ―¹―²–Ψ–Η―² ―΅–Β–Μ–Ψ–≤–Β–Κ ―Ä–Ψ―¹―²–Ψ–Φ 1,8 –Φ, –Β―¹–Μ–Η –¥–Μ–Η–Ϋ–Α –Β–≥–Ψ ―²–Β–Ϋ–Η ―Ä–Α–≤–Ϋ–Α 9 –Φ, –≤―΄―¹–Ψ―²–Α ―³–Ψ–Ϋ–Α―Ä―è 4 –Φ?
–ù–Α –Κ–Α–Κ–Ψ–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η (–≤ –Φ–Β―²―Ä–Α―Ö) –Ψ―² ―³–Ψ–Ϋ–Α―Ä―è ―¹―²–Ψ–Η―² ―΅–Β–Μ–Ψ–≤–Β–Κ ―Ä–Ψ―¹―²–Ψ–Φ 1,8 –Φ, –Β―¹–Μ–Η –¥–Μ–Η–Ϋ–Α –Β–≥–Ψ ―²–Β–Ϋ–Η ―Ä–Α–≤–Ϋ–Α 9 –Φ, –≤―΄―¹–Ψ―²–Α ―³–Ψ–Ϋ–Α―Ä―è 4 –Φ?
 –ü–Β―Ä–Β―Ä–Η―¹―É–Β–Φ –¥–Α–Ϋ–Ϋ―΄–Ι ―Ä–Η―¹―É–Ϋ–Ψ–Κ –≤ –≤–Η–¥–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤ –Η –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ –Η–Ϋ―²–Β―Ä–Β―¹―É―é―â–Η–Β –Ϋ–Α―¹ ―²–Ψ―΅–Κ–Η.
–ü–Β―Ä–Β―Ä–Η―¹―É–Β–Φ –¥–Α–Ϋ–Ϋ―΄–Ι ―Ä–Η―¹―É–Ϋ–Ψ–Κ –≤ –≤–Η–¥–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤ –Η –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ –Η–Ϋ―²–Β―Ä–Β―¹―É―é―â–Η–Β –Ϋ–Α―¹ ―²–Ψ―΅–Κ–Η.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ABC –Η DCE, ―ç―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η
–Ω–Ψ–¥–Ψ–±–Ϋ―΄, ―².–Κ. /C - –Ψ–±―â–Η–Ι, /B –Η /DEC - –Ω―Ä―è–Φ―΄–Β, –Α ―É–≥–Μ―΄ A –Η EDC - ―Ä–Α–≤–Ϋ―΄, ―²–Α–Κ –Κ–Α–Κ ―è–≤–Μ―è―é―²―¹―è
―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Η–Φ–Η.
–‰–Ζ –Ω–Ψ–¥–Ψ–±–Η―è ―ç―²–Η―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤ ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ AB/DE=BC/EC,
AB/DE=(BE+EC)/EC, –Ψ―²―¹―é–¥–Α (AB*EC)/DE=BE+EC
BE=(AB*EC)/DE-EC
BE=(4*9)/1,8-9=11
–û―²–≤–Β―²: ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―³–Ψ–Ϋ–Α―Ä―è –¥–Ψ ―΅–Β–Μ–Ψ–≤–Β–Κ–Α 11 –Φ.
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ AB=8, BC=10, AC=14. –ù–Α–Ι–¥–Η―²–Β cos∠ABC.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ AB=8, BC=10, AC=14. –ù–Α–Ι–¥–Η―²–Β cos∠ABC.
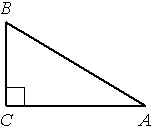 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C –Ω―Ä―è–Φ–Ψ–Ι, BC=4, sinA=0,8. –ù–Α–Ι–¥–Η―²–Β AB.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C –Ω―Ä―è–Φ–Ψ–Ι, BC=4, sinA=0,8. –ù–Α–Ι–¥–Η―²–Β AB.
–ö–Ψ―¹–Η–Ϋ―É―¹ –Ψ―¹―²―Ä–Ψ–≥–Ψ ―É–≥–Μ–Α A ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―Ä–Α–≤–Β–Ϋ 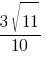 . –ù–Α–Ι–¥–Η―²–Β sinA.
. –ù–Α–Ι–¥–Η―²–Β sinA.
 –Δ–Ψ―΅–Κ–Α O βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä–Ψ–Ι –Μ–Β–Ε–Α―² ―²–Ψ―΅–Κ–Η S, T –Η V ―²–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, ―΅―²–Ψ OSTV βÄ™ ―Ä–Ψ–Φ–±. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ STV. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–Δ–Ψ―΅–Κ–Α O βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä–Ψ–Ι –Μ–Β–Ε–Α―² ―²–Ψ―΅–Κ–Η S, T –Η V ―²–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, ―΅―²–Ψ OSTV βÄ™ ―Ä–Ψ–Φ–±. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ STV. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –Δ–Ψ―΅–Κ–Α O βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä–Ψ–Ι –Μ–Β–Ε–Α―² ―²–Ψ―΅–Κ–Η S, T –Η V ―²–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, ―΅―²–Ψ OSTV βÄ™ ―Ä–Ψ–Φ–±. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ OVT. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–Δ–Ψ―΅–Κ–Α O βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä–Ψ–Ι –Μ–Β–Ε–Α―² ―²–Ψ―΅–Κ–Η S, T –Η V ―²–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, ―΅―²–Ψ OSTV βÄ™ ―Ä–Ψ–Φ–±. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ OVT. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: