В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
По условию задачи треугольник ABC -
равнобедренный.
BM является не только
медианой, но и
высотой (по
третьему свойству равнобедренного треугольника).
Следовательно:
1) AM=MC=AC/2=56/2=28
2) Треугольник ABM
прямоугольный.
Тогда, по
теореме Пифагора:
AB2=BM2+AM2
532=BM2+282
2809=BM2+784
BM2=2025
BM=45
Ответ: 45
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
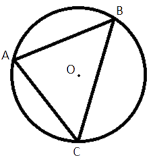Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
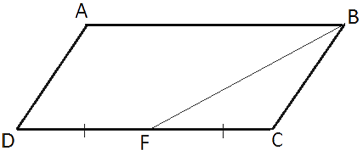Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: