
 Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
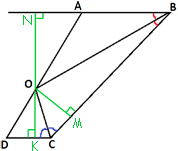 Расстояние от точки О до прямых - это длина перпендикуляра, проведенного от точки до прямой. Иными словами, надо доказать, что ON=OM=OK.
Расстояние от точки О до прямых - это длина перпендикуляра, проведенного от точки до прямой. Иными словами, надо доказать, что ON=OM=OK.
Рассмотрим треугольник NBO.
sin∠NBO=ON/OB (по
определению синуса).
ON=OB*sin∠NBO
Рассмотрим треугольник BMO.
sin∠OBM=OM/OB (по
определению синуса).
OM=OB*sin∠OBM
∠NBO=∠OBM (т.к. OB -
биссектриса).
Следовательно, OM=OB*sin∠OBM=OB*sin∠NBO=ON
Аналогично доказывается, что OK=OM.
Т.е. ON=OM=OK.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
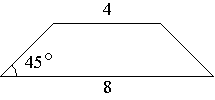 В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
 Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
 В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
Комментарии: