
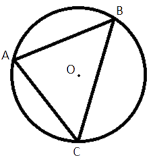 Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
Градусная мера всей окружности 360°.
Разделим ее на равные условные части так, чтобы одна дуга имела 3 такие части, вторая дуга 7 частей, а третья 8 частей (как у условии задачи). Тогда понятно, что нам нужно 3+7+8 таких частей, итого 18.
Градусная мера каждой части равна 360°/18=20°.
Тогда наша первая дуга имеет градусную меру 20°*3=60°, вторая - 20°*7=140°, третья - 20°*8=160°.
Углы ABC, BCA и CAB -
вписанные в окружность, следовательно, они равны половине градусной меры дуги, на которую опираются, т.е.:
Один угол равен 30°, второй 70°, а третий 80°.
По
теореме о соотношении углов и сторон треугольника: на против меньшей стороны лежит меньший угол. Меньший угол равен 30° (это мы только что вычислили), а меньшая сторона равна 20 (по условию задачи).
По
теореме синусов 20/sin30°=2R
20/0,5=2R
40=2R
R=20
Ответ: 20
Поделитесь решением
Присоединяйтесь к нам...
 Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
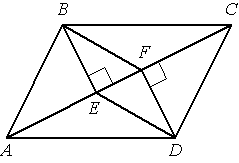 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
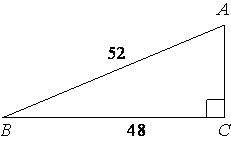 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
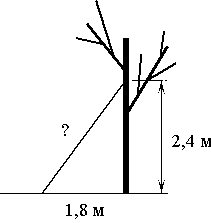 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
Комментарии: