
 Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
 Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту трапеции.
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту трапеции.
Проведем высоту как показано на рисунке. Получившийся треугольник является
прямоугольным. По
определению синуса можем записать: sin30°=h/5 => h=5*sin30°, sin30°=1/2 (
табличное значение).
h=5*1/2=2,5.
Sтрапеции=(3+9)/2*2,5=15
Ответ: площадь трапеции равна 15.
Поделитесь решением
Присоединяйтесь к нам...
 Лестница соединяет точки A и B и состоит из 15 ступеней. Высота каждой ступени равна 28 см, а длина – 96 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 15 ступеней. Высота каждой ступени равна 28 см, а длина – 96 см. Найдите расстояние между точками A и B (в метрах).
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
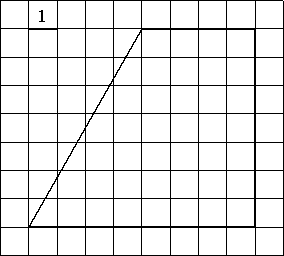 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
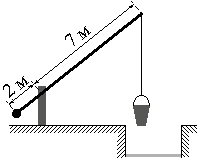 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Комментарии: