
 Точка О – центр окружности, /AOB=72° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=72° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=72°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 72°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 72/2=36.
Ответ: /ACB=36°.
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.
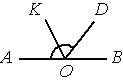 Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
 Один из углов равнобедренной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Один из углов равнобедренной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
 Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата.
Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата.
 ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
Комментарии: