
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.
Рассмотрим каждое утверждение:
1) "Центры
вписанной и описанной окружностей
равнобедренного треугольника совпадают." - это утверждение неверно, т.к. центр вписанной окружности находится внутри треугольника, а центр описанной окружности может находиться вне треугольника (по
теореме об окружности).
2) "Существует
параллелограмм, который не является
прямоугольником." - это утверждение верно, т.к. не противоречит
определению параллелограмма.
3) "Сумма углов
тупоугольного треугольника равна 180°." - это утверждение верно, т.к. не противоречит
теореме о сумме углов треугольника.
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
 Хорды AC и BD окружности пересекаются в точке P, BP=7, CP=14, DP=10. Найдите AP.
Хорды AC и BD окружности пересекаются в точке P, BP=7, CP=14, DP=10. Найдите AP.
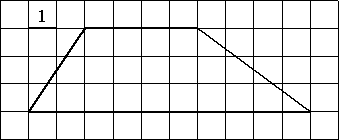 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
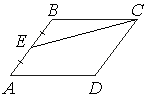 Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Комментарии: