В треугольнике ABC проведена биссектриса AL, угол ALC равен 37°, угол ABC равен 25°. Найдите угол ACB. Ответ дайте в градусах.
Рассмотрим треугольник ABL.
∠BLA=180°-∠ALC=180°-37°=143° (т.к. это
смежные углы)
По
теореме о сумме углов треугольника:
180°=∠ABC+∠BLA+∠LAB=25°+143°+∠LAB
∠LAB=180°-25°-143°=12°
Рассмотрим треугольник ALC.
∠LAC=∠LAB=12° (т.к. AL -
биссектриса)
По
теореме о сумме углов треугольника:
180°=∠ALC+∠ACB+∠LAC=37°+∠ACB+12°
∠ACB=180°-37°-12°=131°
Ответ: 131
Поделитесь решением
Присоединяйтесь к нам...
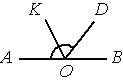Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
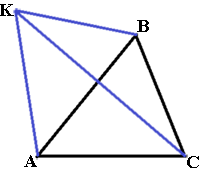Стороны AC, AB, BC треугольника ABC равны 2√
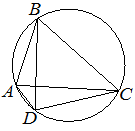Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.
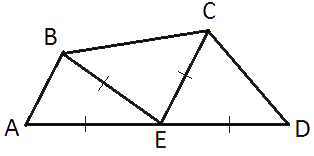Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: