
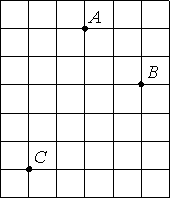
 На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
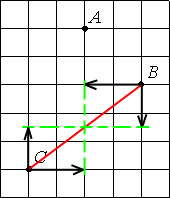 Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
То есть, относительно точки С на 2 клетки вправо и на 1,5 клетки вверх.
Относительно точки В на 2 клетки влево и на 1,5 клетки вниз.
Тогда очевидно, что расстояние от точки А до середины ВС равно 3,5 клетки, т.е. 3,5см
Ответ: 3,5
Поделитесь решением
Присоединяйтесь к нам...
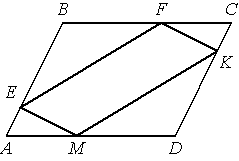 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
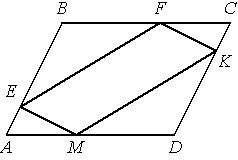 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
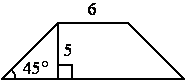 В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=7.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=7.
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 6:5. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 6:5. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Комментарии:
(2017-02-19 17:24:55) Даниил: Спасибо за труды автору, помог!
(2014-05-31 22:06:34) Администратор: ТАНЮШКА, очень рад за Вас, очень рад, что не напрасно создал сайт. Спасибо Вам, что поделились радостью, очень приятно!
(2014-05-31 21:12:02) ТАНЮШКА: Спасибо вам за решение. Благодаря вашему сайту, я смогла решить подобную задачу на реальном гиа(ОГЭ)!