В треугольнике ABC угол C прямой, BC=8, cosB=0,8. Найдите AB.
По
определению косинуса, cosB=ВС/АВ=8/АВ=0,8.
АВ=8/0,8=10.
Ответ: АВ=10.
Поделитесь решением
Присоединяйтесь к нам...
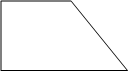Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
В треугольнике ABC угол C равен 90°, AC=10, tgA=0,1. Найдите BC.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
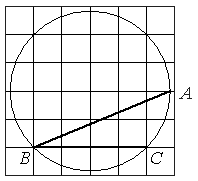Найдите угол ABC. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: