
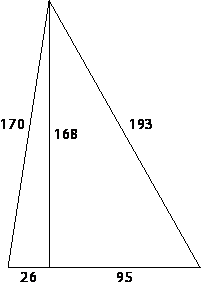 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
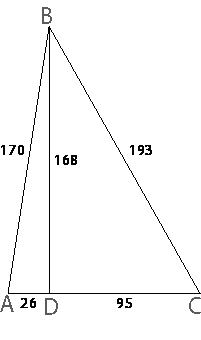 Обозначим ключевые точки как показано на рисунке.
Обозначим ключевые точки как показано на рисунке.
Проверим, является ли BD
высотой данного треугольника. Если является, то треугольник ABD -
прямоугольный и к нему применима
теорема Пифагора:
AB2=AD2+BD2
1702=262+1682
28900=676+28224
28900=28900
Равенство выполняется.
Площадь треугольника равна произведению
высоты на половину стороны, к которой проведена
высота.
SABC=BD*AC/2=BD*(AD+DC)/2=168*(26+95)/2=84*121=10164
Ответ: SABC=10164
Поделитесь решением
Присоединяйтесь к нам...
 Стороны AC, AB, BC треугольника ABC равны 2√
Стороны AC, AB, BC треугольника ABC равны 2√
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
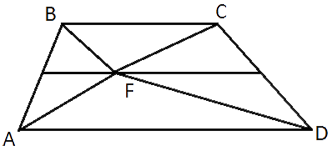 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
 Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
 Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.
Комментарии: