
 Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
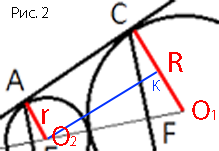
Рассмотрим
трапецию ACO1O2
Данная трапеция
прямоугольная, т.к. радиусы перпендикулярны
касательной AC (по
свойству касательной).
Проведем O2K параллельно AC, O2K=AC, т.к. ACKO2 -
прямоугольник.
 По
теореме Пифагора:
По
теореме Пифагора:
(O1O2)2=(O2K)2+(KO1)2
(R+r)2=(O2K)2+(R-r)2
(90+45)2=(O2K)2+(90-45)2
18225=(O2K)2+2025
(O2K)2=16200
O2K=10√
Рассмотрим треугольники OAO2 и OCO1 (cм. Рис.1).
∠AOO2 - общий
∠OAO2=∠OCO1=90°
Следовательно эти треугольники
подобны (по
первому признаку подобия треугольников).
Тогда, R/r=OC/OA
90/45=OC/OA=(OA+AC)/OA
2*OA=OA+10√
OA=10√
Из
подобия этих же треугольников:
R/r=O10/O2O
R/r=(O2O+R+r)/O2O
90/45=(O2O+90+45)/O2O
2(O2O)=O2O+135
O2O=135
Обозначим угол ∠AOO2 как α
cosα=OA/OO2=10√
Посмотрим на треугольники OAE и OCF.
Они
прямоугольные по
второму свойству хорды.
Тогда для треугольника OAE:
cosα=OE/OA
OE=OA*cosα=10√
Для треугольника OCF:
cosα=OF/OC
OF=OC*cosα=(OA+AC)*cosα=(10√
EF=OF-OE=240-120=120
Ответ: EF=120
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен  . Найдите CosA.
. Найдите CosA.
 В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
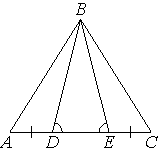 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Комментарии:
(2018-11-23 22:20:48) Администратор: Алевтина, если Вы можете предложить решение проще, напишите нам, будем очень благодарны, не только мы, но и все пользователи. Мы обязательно опубликуем Ваше решение под Вашим именем.
(2018-11-21 22:48:47) алевтина: Вопрос заключается в следующем: почему очень простую и лёгкую задачу, которую можно решить в два действия, Вы решаете сложно и неинтересно???
(2014-05-24 18:44:07) танюшка: Идеально.