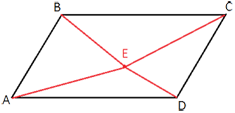
Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
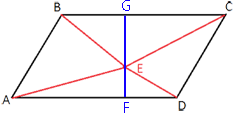Проведем отрезок перпендикулярный сторонам AD и BC, проходящий через точку Е.
Площадь параллелограмма:
SABCD=AD*GF
Площадь треугольника AED:
SAED=AD*EF/2
Площадь треугольника BEC:
SBEC=BC*EG/2
AD=BC (по
свойству параллелограмма).
SBEC+SAED=BC*EG/2+AD*EF/2=AD*EG/2+AD*EF/2=(EG+EF)*AD/2=GF*AD/2=SABCD/2
Поделитесь решением
Присоединяйтесь к нам...
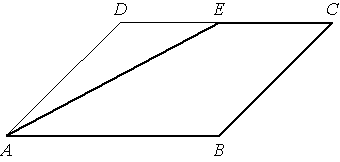Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, описанной около этого треугольника.
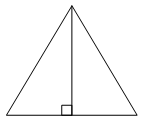Высота равностороннего треугольника равна 78√
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=15, AC=25, NC=22.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-24 12:15:57) Администратор: Так здесь и использована эта формула. AD - основание, GF - высота.
(2015-05-24 12:10:25) : а почему такая формула параллелограмма? ведь формула основание*высоту. понимаю, что я видимо чего-то не знаю, поэтому и прошу пояснить. заранее спасибо!) лучший сайт!)))
(2015-05-23 18:49:23) Администратор: Да, конечно GF, это опечатка. Исправлено. Спасибо, что заметили.
(2015-05-23 17:31:32) : как я поняла..в конце ошибка не ef а gf
(2015-05-23 17:28:36) : обьясните пожалуйста последнюю строку