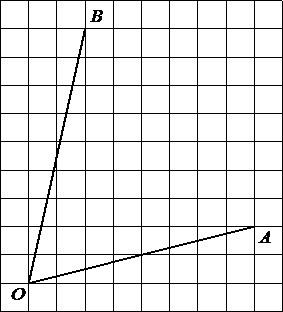Найдите тангенс угла
AOB.
Вариант №1 (Прислал пользователь Евгений)
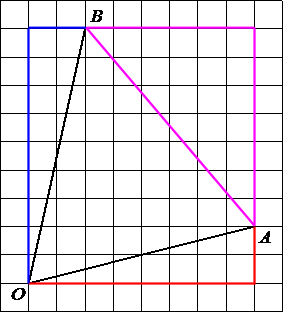Проведем отрезок AB.
Найдем каждую сторону треугольника ABO по
теореме Пифагора:
AO2=22+82
AO2=4+64=68
AO=√
AB2=72+62
AB2=49+36=85
AB=√
BO2=92+22
BO2=81+4=85
BO=√
По
теореме косинусов:
AB2=AO2+BO2-2AO*BO*cos∠AOB
(√
85=4*17+85-4√
85=153-4√
-68=-4√
17=√
cos∠AOB=17/√
По основной тригонометрической формуле:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+(17/√
sin2∠AOB+289/1445=1
sin2∠AOB+17/85=1
sin2∠AOB+1/5=1
sin2∠AOB=4/5
sin∠AOB=2/√
tg∠AOB=sin∠AOB/cos∠AOB=(2/√
Ответ: tg∠AOB=2
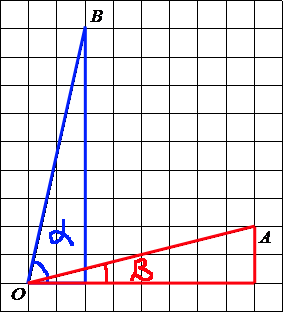Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.Поделитесь решением
Присоединяйтесь к нам...
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
Найдите угол ABC . Ответ дайте в градусах.
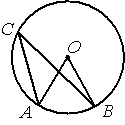Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Площадь равнобедренного треугольника равна 144√
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-16 19:18:34) Светлана: Полностью согласна с Еленой. Для учащихся 9 класса её способ в ЭТОЙ задаче рациональней!
(2015-04-06 22:41:10) Администратор: Елена, про формулу я согласен, поэтому и опубликовал другой способ - через теорему синусов. К 397 задаче я оставил свой комментарий, но повторю его и здесь. Любая неточность в рисунке, и Вам придется несколько раз применять теорему Пифагора, чтобы найти перпендикуляр. Я не считаю этот метод правильным. Через теорему косинусов - это универсальный способ: 1) Математически точен, 2) не надо на рисунке пытаться достраивать перпендикуляр, 3) это не так долго. как может показаться, просто я подробно расписываю каждое действие.
(2015-04-06 21:34:32) Елена: Сам подход только через теорему Пифагора универсален. В 9 классе ещё не изучают тригонометрические формулы, за исключением основного тригонометрического тождества. Да не везде равнобедренный треугольник, тогда смотри комментарии к 397 задаче (она решается также, как задача 482). Время для решения первой части экзамена ограниченно, а с теоремой косинусов нужно повозиться.
(2015-04-06 20:42:05) Администратор: Елена, для данной задачи получится так решить, но решение не универсально. Не во всех задачах задан равнобедренный треугольник. Эту и аналогичные задачи можно решить по теореме косинусов (как задачу №482)
(2015-04-06 16:55:18) Елена: Треугольник OBA равнобедренный, т.к. OB=AB ( находим их по теореме Пифагора , как диагонали соответствующих им прямоугольников). По клеткам явно видно середину OA (назовём её M). В равнобедренном треугольнике медиана является высотой, значит треугольник OMB прямоугольный. По определению тангенса tgAOB=BM/OM. Находим диагонали BM и OM из соответствующих прямоугольников и ответ: 2. Придётся поработать с корнями, зато не надо заучивать формулу тангенса разности двух углов.