Найдите угол ABC. Ответ дайте в градусах.
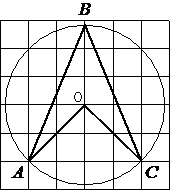Проведем два отрезка к центру окружности как показано на рисунке.
По координатной сетке видно, что получившийся угол AOC прямой, т.е. равен 90°.
∠AOC является
центральным для окружности, следовательно градусная мера дуги, на которую он опирается, тоже равна 90°.
∠ABC -
вписанный угол и по
теореме равен 90°/2=45°
Ответ: ∠ABC=45°
Поделитесь решением
Присоединяйтесь к нам...
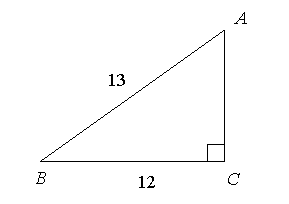Найдите площадь треугольника, изображённого на рисунке.
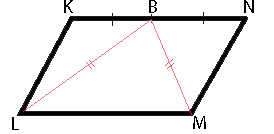В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов остроугольного треугольника равна 180°.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-16 19:10:55) Светлана: По свойству вписанных углов данный угол замените равным, опирающимся на ту же самую дугу АС (Вершина такого угла будет лежать четырьмя точками выше от точки А). В полученном прямоугольном треугольнике катеты равны, значит он ещё и равнобедренный. угол равен 45.
(2015-04-06 22:43:44) Администратор: Елена, да, можно и так.
(2015-04-06 18:52:31) Елена: По сетке видно, что дуга АС-это четвёртая часть окружности, значит дуга АС равна 90 градусов. Вписанный угол АВС равен половине дуги на которую он опирается, значит 45 градусов