Найдите угол ABC. Ответ дайте в градусах.
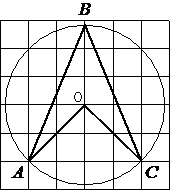Проведем два отрезка к центру окружности как показано на рисунке.
По координатной сетке видно, что получившийся угол AOC прямой, т.е. равен 90°.
∠AOC является
центральным для окружности, следовательно градусная мера дуги, на которую он опирается, тоже равна 90°.
∠ABC -
вписанный угол и по
теореме равен 90°/2=45°
Ответ: ∠ABC=45°
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Любой квадрат является ромбом.
2) Против равных сторон треугольника лежат равные углы.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Прямая касается окружности в точке K. Центр окружности – точка O. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах.
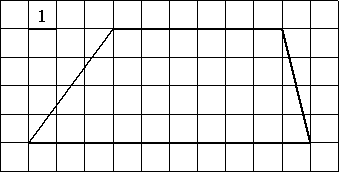Найдите площадь трапеции, изображённой на рисунке.
Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-16 19:10:55) Светлана: По свойству вписанных углов данный угол замените равным, опирающимся на ту же самую дугу АС (Вершина такого угла будет лежать четырьмя точками выше от точки А). В полученном прямоугольном треугольнике катеты равны, значит он ещё и равнобедренный. угол равен 45.
(2015-04-06 22:43:44) Администратор: Елена, да, можно и так.
(2015-04-06 18:52:31) Елена: По сетке видно, что дуга АС-это четвёртая часть окружности, значит дуга АС равна 90 градусов. Вписанный угол АВС равен половине дуги на которую он опирается, значит 45 градусов