
 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
По
определению тангенса, tgB=7/2=3,5
Ответ: tgB=3,5.
Поделитесь решением
Присоединяйтесь к нам...
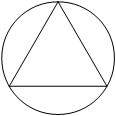 Сторона равностороннего треугольника равна 2√
Сторона равностороннего треугольника равна 2√
 Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
 Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Косинус острого угла А треугольника равен 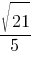 . Найдите sinA.
. Найдите sinA.
Комментарии:
(2015-05-21 20:40:29) Администратор: Лена, по определению tg - это отношение ПРОТИВОлежащего катета к ПРИлежащему, поэтому 7/2.
(2015-05-20 16:30:44) Лена: Почему 7/2,а не 2/7?