
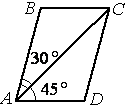 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
По
свойству
параллелограмма /A=/C=45°+30°=75° и /B=/D.
Найдем углы B и D.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть AC как секущую к этим параллельным прямым, то становится очевидным, что /DAC=/BCA=45° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABC.
По
теореме о сумме углов треугольника мы можем написать: 180°=/CAB+/B+/BCA
180°=30°+/B+45°
/B=105°=/D
105>75, следовательно углы B и D - бОльшие.
Ответ: больший угол равен 105°.
Поделитесь решением
Присоединяйтесь к нам...
 Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
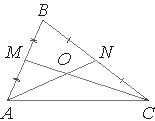 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
 Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
 Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Комментарии: