Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
По свойству
равнобедренной трапеции - углы при основании равны. Тогда /ABC=/BCD=25°+100°=125°.
Сумма углов четырехугольника равна 360°, тогда получаем, что 360° = 125° + 125° + /BAD + /ADC,
/BAD+/ADC=360°-125°-125°=110°, а учитывая, что /BAD=/ADC (по тому же
свойству равнобедренной трапеции), получаем /BAD=/ADC=110°/2=55°, эти углы и есть меньшие в трапеции
Ответ: меньший угол трапеции = 55°.
Поделитесь решением
Присоединяйтесь к нам...
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
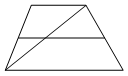Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
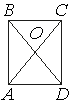Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-24 18:26:39) Администратор: Аида, Вы забыли еще про два угла, посмотрите повнимательней.
(2015-05-24 17:11:43) Аида: 125+125= 250 же будет,почему вы 360 написали?