
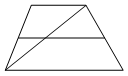
 Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
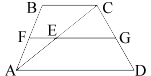 Обозначим ключевые точки, как показано на рисунке.
Обозначим ключевые точки, как показано на рисунке.
Рассмотрим треугольник ABC.
AF=FB (по
определению средней линии трапеции).
Тогда, по теореме Фалеса:
AE=EC
Получается, что FE -
средняя линия треугольника ABC.
FE=BC/2=8/2=4 (по
теореме о средней линии треугольника).
Рассмотрим треугольник ACD.
Аналогично, EG -
средняя линия данного треугольника, следовательно EG=AD/2=18/2=9.
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
 ABCDEFGHI – правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
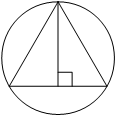 Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Комментарии: