
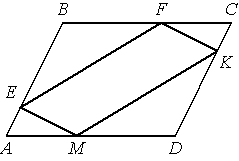
 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
1) Рассмотрим треугольники АЕМ и CKF.
АЕ=CK (по условию задачи)
/A=/C (по
свойству параллелограмма)
СF=АM (по условию задачи).
Следовательно, треугольники АЕМ и CKF равны (по первому признаку).
Поэтому ЕМ=FK.
2) Рассмотрим треугольники EBF и KDM.
Т.к. AB=CD и AD=BC (по
свойству параллелограмма), а АЕ = CK и СF = АM (по условию задачи), то BE=KD и BF=DM.
/B=/D (по
свойству параллелограмма).
Следовательно, треугольники EBF и KDM (по первому признаку). А это значит, что EF=KM.
Из пунктов 1 и 2 (равенство сторон) следует, что EFKM —
параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
 Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
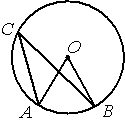 Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
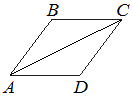 В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
 В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
 На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
Комментарии: