Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Рассмотрим каждое утверждение:
1) "Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны". Это утверждение верно по
первому признаку подобия.
2) "Вертикальные углы равны", это утверждение верно, по
свойству углов.
3) "Любая биссектриса равнобедренного треугольника является его медианой", это утверждение неверно, т.к., по
свойству равнобедренного треугольника, только
биссектриса, проведенная к основанию, совпадает с
медианой и высотой.
Поделитесь решением
Присоединяйтесь к нам...
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
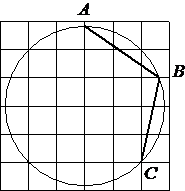Найдите угол ABC . Ответ дайте в градусах.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-01-26 23:57:40) Администратор: Анастасия, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-25 18:27:37) Анастасия: Какие из следующих утверждений верны? 1.Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу. 2.Площади трапеции равна произведению основания трапеции на высоты. 3.Треугольника со сторонами 1,2,4 не существуют.