
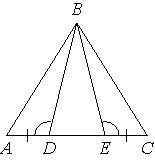
 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
1) По условию задачи /ADB=/BEC, следовательно,
смежные им углы /BDE и /BEС тоже равны друг другу.
Тогда треугольник BDE -
равнобедренный (по
свойству).
Следовательно, BD=DE, по
определению равнобедренного треугольника.
2) Рассмотрим треугольники ABD и CBE.
AD=CE (по условию),
BD=BE (согласно п.1),
/ADB=/BEC (по условию),
следовательно эти треугольники равны (по
первому признаку равенства треугольников), а это значит, что BA=BC. Следовательно треугольник ABC - равнобедренный (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
 Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
 Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
 Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
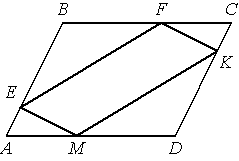 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
 В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
Комментарии: