
 Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
Рассмотрим треугольник АОВ. АО=ОВ, т.к. это радиусы окружности. Следовательно,
треугольник АОВ - равнобедренный. Следовательно, /ОВА = /ОАВ (по свойству равнобедренного треугольника). По теореме о сумме углов треугольника 180°=/AOB+/ОАВ+/ОBA. => /ОАВ+/ОBA=180°-60°=120°
А т.к. /ОАВ=/ОBA, то /ОАВ=/ОBA=120°/2=60°
Следовательно треугольник АОВ - равносторонний (по свойству равностороннего треугольника). Следовательно, R=ОВ=ОА=АВ=5.
Ответ: AB=5.
Поделитесь решением
Присоединяйтесь к нам...
 Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
 Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
 Площадь прямоугольного треугольника равна 2√
Площадь прямоугольного треугольника равна 2√
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=6, AD=13, AC=38. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=6, AD=13, AC=38. Найдите AO.
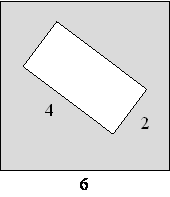 Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Комментарии:
(2015-04-28 19:33:07) Администратор: Иван, спасибо, что заметили опечатку. Ответ тот же, но замечание верное. еще раз спасибо!
(2015-04-28 16:44:20) Иван: Почему Ответ: R=5?Когда нам надо найти длину хорды AB