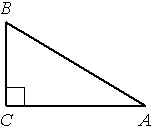
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.

Другие задачи из этого раздела

Задача №A0C43B

Окружности радиусов 3 и 33 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Задача №B7BF5D

На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.

Задача №1CA1CE

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.

Задача №ED3921

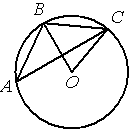Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).

Задача №C3668A

Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.