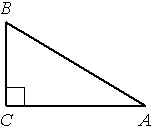
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
По
определению синуса sinA=BC/AB => AB=BC/sinA=4/0,8=5.
Ответ: AB=5.
Поделитесь решением
Присоединяйтесь к нам...
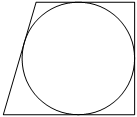Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
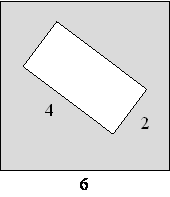Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: