
 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
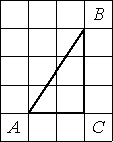
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
По
определению тангенса: tgA=BC/AC=3/2=1,5.
Ответ: tgA=1,5.
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь трапеции, изображённой на рисунке.
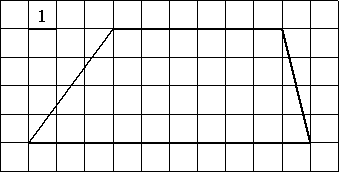
Найдите площадь трапеции, изображённой на рисунке.
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
 Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BKC.
Укажите номера верных утверждений.
1) Существует прямоугольник, который не является параллелограммом.
2) Треугольник с углами 40° , 70°, 70° — равнобедренный.
3) Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны.
Комментарии:
(2016-04-03 15:12:32) glybin: Спасибо!