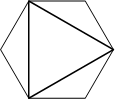
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
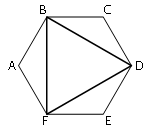Рассмотрим треугольники FAB, BCD и DEF.
Т.к. шестиугольник
правильный, то FA=AB=BC=CD=DE=EF и углы /FAB=/BCD=/DEF. Значит рассматриваемые треугольники равны (по
первому признаку равенства). Следовательно, FB=BD=DF. Т.е. треугольник BDF -
равносторонний.
Поделитесь решением
Присоединяйтесь к нам...
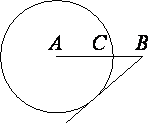На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K,
длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
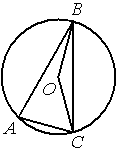Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: