
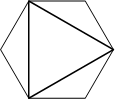
 Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
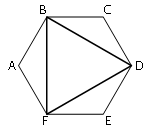 Рассмотрим треугольники FAB, BCD и DEF.
Рассмотрим треугольники FAB, BCD и DEF.
Т.к. шестиугольник
правильный, то FA=AB=BC=CD=DE=EF и углы /FAB=/BCD=/DEF. Значит рассматриваемые треугольники равны (по
первому признаку равенства). Следовательно, FB=BD=DF. Т.е. треугольник BDF -
равносторонний.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C прямой, BC=6, sinA=0,6. Найдите AB.
В треугольнике ABC угол C прямой, BC=6, sinA=0,6. Найдите AB.
 В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
 Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
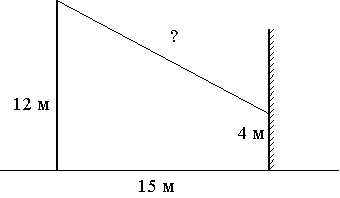 От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
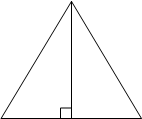 Высота равностороннего треугольника равна 96√
Высота равностороннего треугольника равна 96√
Комментарии: