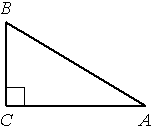
В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
По
определению синуса sinA=BC/AB => AB=BC/sinA=9/0,3=30.
Ответ: AB=30.
Поделитесь решением
Присоединяйтесь к нам...
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=40.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
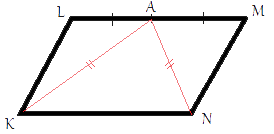В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
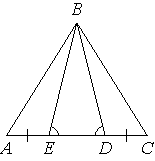На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: