
 Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
По
определению тангенса: tgС=AB/AC=3/6=1/2=0,5.
Ответ: tgС=0,5.
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
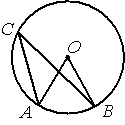 Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
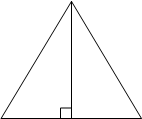 Высота равностороннего треугольника равна 96√
Высота равностороннего треугольника равна 96√
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
 В треугольнике ABC угол C прямой, BC=6, sinA=0,6. Найдите AB.
В треугольнике ABC угол C прямой, BC=6, sinA=0,6. Найдите AB.
Комментарии:
(2015-05-24 18:20:11) Администратор: Диана, это опечатка, спасибо, что заметили. Исправлено.
(2015-05-24 14:10:07) Диана: А почему написано tgA в решении?