
Постройте график функции y=2x+4|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
 2x+4x-x2, при x≥0
2x+4x-x2, при x≥0
2x+4(-x)-x2, при x<0
 6x-x2, при x≥0
6x-x2, при x≥0
-2x-x2, при x<0
Рассмотрим и построим график для каждой подфункции и объединим их.
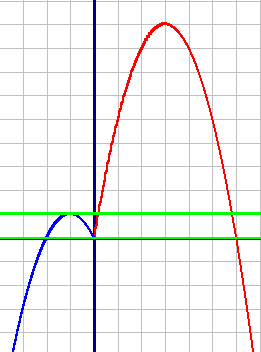 1) y1=6x-x2, при x≥0 (красный график)
1) y1=6x-x2, при x≥0 (красный график)
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 0 | 5 | 8 | 9 | 8 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 1 | 0 | -3 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=x2-6|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Постройте график функции y=|x2+5x+6| . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
 При работе фонарика батарейка постепенно разряжается и напряжение
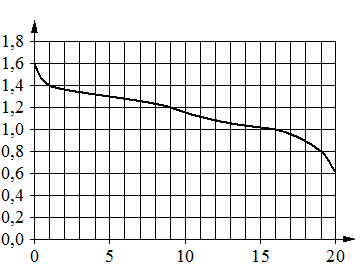
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение за первые 16 часов работы фонарика.
При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение за первые 16 часов работы фонарика.
Известно, что графики функций y=x2+p и y=2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) a<0, c>0 2) a<0, c<0 3) a>0, c<0 4) a>0, c>0 |
А)  |
Б)  |
В)  |
Комментарии: