
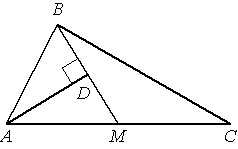
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
AD для треугольника ABM является и
медианой, и высотой. А это
свойство медианы для равнобедренного треугольника. Следовательно, треугольник ABM -
равнобедренный с основанием BM.
По
определению равнобедренного треугольника AB=AM.
Т.к. BM - медиана для треугольника ABC, следовательно AM=MC (по
определению медианы).
Тогда AM=AC/2=5. Как мы выяснили ранее AM=AB => AB=5.
Ответ: AB=5.
Поделитесь решением
Присоединяйтесь к нам...
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
 Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
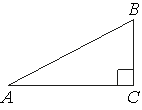 В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
 В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.
Комментарии: