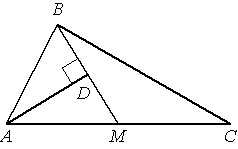
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
AD для треугольника ABM является и
медианой, и высотой. А это
свойство медианы для равнобедренного треугольника. Следовательно, треугольник ABM -
равнобедренный с основанием BM.
По
определению равнобедренного треугольника AB=AM.
Т.к. BM - медиана для треугольника ABC, следовательно AM=MC (по
определению медианы).
Тогда AM=AC/2=5. Как мы выяснили ранее AM=AB => AB=5.
Ответ: AB=5.
Поделитесь решением
Присоединяйтесь к нам...
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
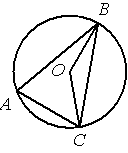Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
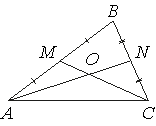Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
Стороны AC, AB, BC треугольника ABC равны 2√
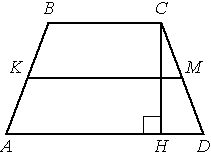В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: