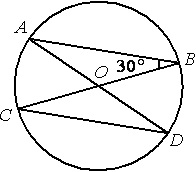В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
Вариант 1. Предложил пользователь Татьяна.
∠ABO=∠ABC=30°
∠ODC=∠ADC
Оба этих угла являются
вписанными и опираются на одну и ту же дугу, следовательно (по
второму свойству) они равны:
∠ABC=∠ADC=∠ODC=30°
Ответ: 30
Вариант 2.
Рассмотрим треугольник ABO. Этот треугольник
равнобедренный, т.к. ОA и ОB - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/OBA.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=30°
Ответ: /ODC=30°.
Поделитесь решением
Присоединяйтесь к нам...
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
Синус острого угла A треугольника ABC равен 
. Найдите CosA.
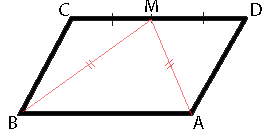В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
Косинус острого угла A треугольника ABC равен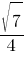 
. Найдите sinA.
В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-11-29 23:20:48) Администратор: Татьяна, да, Вы совершенно правы. Я добавлю Ваш вариант решения на сайт.
(2014-11-29 23:09:15) Татьяна: А нельзя ли эту задачу решить проще?Ведь угол ОДС и АВО - вписанные и опирающиеся на одну дугу. Следовательно, они равны, поэтому угол ОДС=30 градусов.